Restricted Boltzmann machine
A restricted Boltzmann machine, commonly abbreviated as RBM, is a neural network where neurons beyond the visible have probabilitistic outputs. The machine is restricted because connections are restricted to be from one layer to the next, that is, having no intra-layer connections.
Model
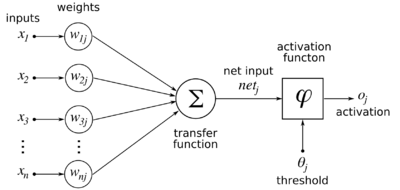
We use a set of binary-valued neurons. Given a set of k-dimensional inputs represented as a column vector <math>\vec{x} = [x_1, x_2, \cdots, x_k]^T</math>, and a set of m neurons with (initially random, between -0.01 and 0.01) synaptic weights from the inputs, represented as a matrix formed by m weight column vectors (i.e. a k row x m column matrix):
w_{11} & w_{12} & \cdots & w_{1m}\\ w_{21} & w_{22} & \cdots & w_{2m}\\ \vdots & & & \vdots \\ w_{k1} & w_{m2} & \cdots & w_{km}
\end{bmatrix}</math>where <math>w_{ij}</math> is the weight between input i and neuron j, the output of the set of neurons is defined as follows:
where <math>\varphi \left ( \cdot \right )</math> is the logistic sigmoidal function:
From this output, a binary-valued reconstruction of the input <math>\vec{x'}</math> is formed as follows:
To update the weights, a set of inputs are presented, the outputs generated, and the inputs reconstructed. Then an average is taken over the results, and the weights are updated as follows:
where <math>\eta</math> is some learning rate and the subscript <math>N</math> indicates that the average is taken over <math>N</math> input presentations. In practice, the reconstruction is then fed back to the input layer and another cycle is run, for several cycles.