Difference between revisions of "Restricted Boltzmann machine"
| Line 7: | Line 7: | ||
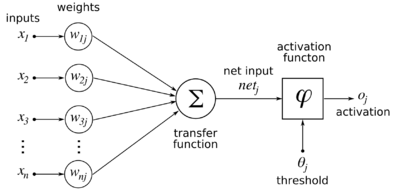
[[File:ArtificialNeuronModel english.png|thumb|right|400px|Model of a neuron. <i>j</i> is the index of the neuron when there is more than one neuron. For the RBM, the activation function is logistic, and the activation is actually the probability that the neuron will fire.]] | [[File:ArtificialNeuronModel english.png|thumb|right|400px|Model of a neuron. <i>j</i> is the index of the neuron when there is more than one neuron. For the RBM, the activation function is logistic, and the activation is actually the probability that the neuron will fire.]] | ||
| − | We use a set of binary-valued neurons. Given a set of k-dimensional inputs represented as a column vector | + | We use a set of binary-valued neurons. Given a set of k-dimensional inputs represented as a column vector [[File:Hebb1.png]], and a set of <i>m</i> neurons with (initially random, between -0.01 and 0.01) synaptic weights from the inputs, represented as a matrix formed by <i>m</i> weight column vectors (i.e. a <i>k</i> row x <i>m</i> column matrix): |
| − | + | [[File:Sanger1.png|center]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | where | + | where [[File:Sanger2.png]] is the weight between input <i>i</i> and neuron <i>j</i>. |
During the positive phase, the output of the set of neurons is defined as follows: | During the positive phase, the output of the set of neurons is defined as follows: | ||
| − | + | [[File:RBM1.png|center]] | |
| − | where | + | where [[File:RBM2.png]] is a column vector of probabilities, where element <em>i</em> indicates the probability that neuron <em>i</em> will output a 1. [[File:RBM3.png]] is the logistic sigmoidal function: |
| − | + | [[File:RBM4.png]] | |
| + | During the negative phase, from this output, a binary-valued ''reconstruction'' of the input [[File:RBM5.png]] is formed as follows. First, choose the binary outputs of the output neurons [[File:RBM6.png]] based on the probabilities [[File:RBM2.png]]. Then: | ||
| − | + | [[File:RBM7.png]] | |
| − | + | Then the reconstructed binary inputs [[File:RBM5.png]] based on the probabilities [[File:RBM8.png]]. Next, the binary outputs [[File:RBM9.png]] are computed again based on the probabilities [[File:RBM10.png]], but this time from the reconstructed input: | |
| − | + | [[File:RBM11.png|center]] | |
| − | + | ||
| − | + | ||
This completes one ''wake-sleep'' cycle. | This completes one ''wake-sleep'' cycle. | ||
| Line 39: | Line 33: | ||
To update the weights, a wake-sleep cycle is completed, and weights updated as follows: | To update the weights, a wake-sleep cycle is completed, and weights updated as follows: | ||
| − | + | [[File:RBM12.png|center]] | |
| − | where | + | where η is some learning rate. In practice, several wake-sleep cycles can be run before doing the weight update. This is known as ''Gibbs sampling''. |
A batch update can also be used, where some number of patterns less than the full input set (a ''mini-batch'') are uniformly randomly presented, the wake and sleep results recorded, and then the updates done as follows: | A batch update can also be used, where some number of patterns less than the full input set (a ''mini-batch'') are uniformly randomly presented, the wake and sleep results recorded, and then the updates done as follows: | ||
| − | + | [[File:RBM13.png|center]] | |
| − | where | + | where [[File:RBM14.png]] is an average over the input presentations. This method is called ''contrastive divergence''. |
| Line 53: | Line 47: | ||
==References== | ==References== | ||
| − | * | + | * Hinton, Geoffrey (August 2, 2010). [http://www.cs.toronto.edu/~hinton/absps/guideTR.pdf "A practical guide to training restricted Boltzmann machines"]. University of Toronto Department of Computer Science. |
| + | |||
| + | * Cho, KyungHyun (March 14, 2011) [http://lib.tkk.fi/Dipl/2011/urn100427.pdf "Improved Learning Algorithms for Restricted Boltzmann Machines"]. Aalto University. | ||
| − | + | [[Category: Neural computational models]] | |
Revision as of 15:24, 24 June 2014
A restricted Boltzmann machine, commonly abbreviated as RBM, is a neural network where neurons beyond the visible have probabilitistic outputs. The machine is restricted because connections are restricted to be from one layer to the next, that is, having no intra-layer connections.
As with contrastive Hebbian learning, there are two phases to the model, a positive phase, or wake phase, and a negative phase, or sleep phase.
Model
During the positive phase, the output of the set of neurons is defined as follows:
This completes one wake-sleep cycle.
To update the weights, a wake-sleep cycle is completed, and weights updated as follows:
where η is some learning rate. In practice, several wake-sleep cycles can be run before doing the weight update. This is known as Gibbs sampling.
A batch update can also be used, where some number of patterns less than the full input set (a mini-batch) are uniformly randomly presented, the wake and sleep results recorded, and then the updates done as follows:
References
- Hinton, Geoffrey (August 2, 2010). "A practical guide to training restricted Boltzmann machines". University of Toronto Department of Computer Science.
- Cho, KyungHyun (March 14, 2011) "Improved Learning Algorithms for Restricted Boltzmann Machines". Aalto University.