Difference between revisions of "Oja's rule"
From Eyewire
| Line 1: | Line 1: | ||
| + | <translate> | ||
| + | |||
'''Oja's rule''', developed by Finnish computer scientist Erkki Oja in 1982, is a stable version of [[Hebb's rule]].<ref name="Oja82">Oja, Erkki (November 1982). [http://www.springerlink.com/content/u9u6120r003825u1 "Simplified neuron model as a principal component analyzer"]. <em>Journal of Mathematical Biology</em> <strong>15</strong> (3): 267–273</ref> | '''Oja's rule''', developed by Finnish computer scientist Erkki Oja in 1982, is a stable version of [[Hebb's rule]].<ref name="Oja82">Oja, Erkki (November 1982). [http://www.springerlink.com/content/u9u6120r003825u1 "Simplified neuron model as a principal component analyzer"]. <em>Journal of Mathematical Biology</em> <strong>15</strong> (3): 267–273</ref> | ||
| Line 21: | Line 23: | ||
[[Category: Neural computational models]] | [[Category: Neural computational models]] | ||
| + | |||
| + | </translate> | ||
Latest revision as of 03:23, 24 June 2016
Oja's rule, developed by Finnish computer scientist Erkki Oja in 1982, is a stable version of Hebb's rule.[1]
Model
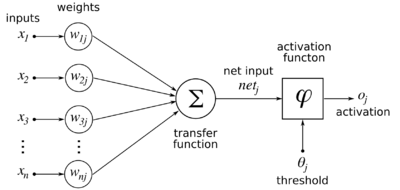
As with Hebb's rule, we use a linear neuron. Given a set of k-dimensional inputs represented as a column vector
Error creating thumbnail: Unable to save thumbnail to destination
, and a linear neuron with (initially random) synaptic weights from the inputs Error creating thumbnail: Unable to save thumbnail to destination
the output the neuron is defined as follows:
Error creating thumbnail: Unable to save thumbnail to destination
Oja's rule gives the update rule which is applied after an input pattern is presented:
Error creating thumbnail: Unable to save thumbnail to destination
Error creating thumbnail: Unable to save thumbnail to destination
ignored for n>1 since η is small.
It can be shown that Oja's rule extracts the first principal component of the data set. If there are many Oja's rule neurons, then all will converge to the same principal component, which is not useful. Sanger's rule was formulated to get around this issue.
References
- ↑ Oja, Erkki (November 1982). "Simplified neuron model as a principal component analyzer". Journal of Mathematical Biology 15 (3): 267–273