Feedforward backpropagation
Feedforward backpropagation is an error-driven learning technique popularized in 1986 by David Rumelhart (1942-2011), an American psychologist, Geoffrey Hinton (1947-), a British informatician, and Ronald Williams, an American professor of computer science.[1] It is a supervised learning technique, meaning that the desired outputs are known beforehand, and the task of the network is to learn to generate the desired outputs from the inputs.
Model
Given a set of k-dimensional inputs represented as a column vector:
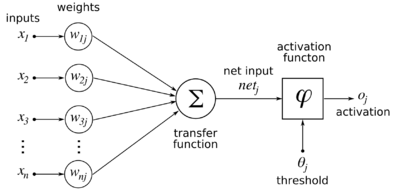
and a nonlinear neuron with (initially random, uniformly distributed between -1 and 1) synaptic weights from the inputs:
then the output of the neuron is defined as follows:
where <math>\varphi \left ( \cdot \right )</math> is a sigmoidal function. We will assume that the sigmoidal function is the simple logistic function:
This function has the useful property that
Feedforward backpropagation is typically applied to multiple layers of neurons, where the inputs are called the input layer, the layer of neurons taking the inputs is called the hidden layer, and the next layer of neurons taking their inputs from the outputs of the hidden layer is called the output layer. There is no direct connectivity between the output layer and the input layer.
If there are <math>N_I</math> inputs, <math>N_H</math> hidden neurons, and <math>N_O</math> output neurons, and the weights from inputs to hidden neurons are <math>w_{Hij}</math> (<math>i</math> being the input index and <math>j</math> being the hidden neuron index), and the weights from hidden neurons to output neurons are <math>w_{Oij}</math> (<math>i</math> being the hidden neuron index and <math>j</math> being the output neuron index), then the equations for the network are as follows:
n_{Hj} &= \sum_{i=1}^{N_I} w_{Hij} x_i, j \in \left \{ 1, 2, \cdots, N_H \right \} \\ y_{Hj} &= \varphi \left ( n_{Hj} \right ) \\ n_{Oj} &= \sum_{i=1}^{N_H} w_{Oij} y_{Hi}, j \in \left \{ 1, 2, \cdots, N_O \right \} \\ y_{Oj} &= \varphi \left ( n_{Oj} \right )\\
\end{align}</math>
If the desired outputs for a given input vector are <math>t_j, j \in \left \{ 1, 2, \cdots, N_O \right \}</math>, then the update rules for the weights are as follows:
\delta_{Oj} &= \left ( t_j-y_{Oj} \right )\\ \Delta w_{Oij} &= \eta y_{Hi} \delta_{Oj}\\ \delta_{Hj} &= y_{Hj} \left ( 1-y_{Hj} \right ) \sum_{k=1}^{N_O} \delta_{Ok} w_{Hjk}\\ \Delta w_{Hij} &= \eta x_i \delta_{Hj}
\end{align}</math>where <math>\delta_{Oj}</math> is an error term for output neuron <math>j</math> and <math>\delta_{Hj}</math> is a backpropagated error term for hidden neuron <math>j</math>.
Derivation
We first define an error term which is the cross-entropy of the output and target. We use cross-entropy because, in a sense, each output neuron represents a hypothesis about what the input represents, and the activation of the neuron represents a probability that the hypothesis is correct.
Next, we determine how the error changes based on changes to an individual weight from hidden neuron to output neuron:
\frac{\mathrm{d} E }{\mathrm{d} w_{Oij}} &= \frac{\mathrm{d} E }{\mathrm{d} y_{Oj}} \frac{\mathrm{d} y_{Oj} }{\mathrm{d} n_{Oj}} \frac{\partial n_{Oj}}{\partial w_{O_ij}} \\ &= - \left [ \frac{t_j}{y_{Oj}} - \frac{1-t_j}{1-y_{Oj}} \right ] \frac{\mathrm{d} \varphi }{\mathrm{d} n_{Oj}} y_{Hi} \\ &= - \left [ \frac{t_j}{y_{Oj}} - \frac{1-t_j}{1-y_{Oj}} \right ] \varphi \left ( n_{Oj} \right ) \left ( 1 - \varphi \left ( n_{Oj} \right ) \right ) y_{Hi} \\ &= - \left [ \frac{t_j}{y_{Oj}} - \frac{1-t_j}{1-y_{Oj}} \right ] y_{Oj} \left ( 1-y_{Oj} \right ) y_{Hi} \\ &= \left ( y_{Oj} - t_j \right ) y_{Hi}
\end{align}</math>We then want to change <math>w_{Oij}</math> slightly in the direction which reduces <math>E</math>, that is, <math>\Delta w_{Oij} \propto - \mathrm{d} E / \mathrm{d} w_{Oij}</math>. This is called gradient descent.
References
- ↑ Script error: No such module "Citation/CS1".