Feedforward backpropagation
Feedforward backpropagation is an error-driven learning technique popularized in 1986 by David Rumelhart (1942-2011), an American psychologist, Geoffrey Hinton (1947-), a British informatician, and Ronald Williams, an American professor of computer science.[1]
Model
Given a set of k-dimensional inputs represented as a column vector:
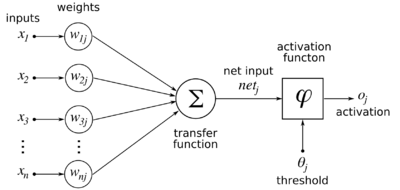
and a nonlinear neuron with (initially random, uniformly distributed between -1 and 1) synaptic weights from the inputs:
then the output of the neuron is defined as follows:
where <math>\varphi \left ( \cdot \right )</math> is a sigmoidal function. We will assume that the sigmoidal function is the simple logistic function:
This function has the useful property that
Feedforward backpropagation is typically applied to multiple layers of neurons, where the inputs are called the input layer, the layer of neurons taking the inputs is called the hidden layer, and the next layer of neurons taking their inputs from the outputs of the hidden layer is called the output layer. There is no direct connectivity between the output layer and the input layer.
If there are <math>N_I</math> inputs, <math>N_H</math> hidden neurons, and <math>N_O</math> output neurons, and the weights from inputs to hidden neurons are <math>w_{Hij}</math> (<math>i</math> being the input index and <math>j</math> being the hidden neuron index), and the weights from hidden neurons to output neurons are <math>w_{Oij}</math> (<math>i</math> being the hidden neuron index and <math>j</math> being the output neuron index), then the equations for the network are as follows:
y_{Hj} &= \varphi \left ( \sum_{i=1}^{N_I} w_{Hij} x_i \right ), j \in \left \{ 1, 2, \cdots, N_H \right \} \\ y_{Oj} &= \varphi \left ( \sum_{i=1}^{N_H} w_{Oij} y_{Hi} \right ), j \in \left \{ 1, 2, \cdots, N_O \right \} \\
\end{align}</math>
References
- ↑ Script error: No such module "Citation/CS1".