Difference between revisions of "Feedforward backpropagation"
| (3 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | <translate> | ||
| + | |||
'''Feedforward backpropagation''' is an error-driven learning technique popularized in 1986 by David Rumelhart (1942-2011), an American psychologist, Geoffrey Hinton (1947-), a British informatician, and Ronald Williams, an American professor of computer science.<ref name=Rumelhart1986>Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J. (October 8, 1986). [http://www.cs.toronto.edu/~hinton/absps/naturebp.pdf "Learning representations by back-propagating errors"] <em>Nature</em> <strong>323</strong> (6088): 533–536</ref> It is a ''supervised'' learning technique, meaning that the desired outputs are known beforehand, and the task of the network is to learn to generate the desired outputs from the inputs. | '''Feedforward backpropagation''' is an error-driven learning technique popularized in 1986 by David Rumelhart (1942-2011), an American psychologist, Geoffrey Hinton (1947-), a British informatician, and Ronald Williams, an American professor of computer science.<ref name=Rumelhart1986>Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J. (October 8, 1986). [http://www.cs.toronto.edu/~hinton/absps/naturebp.pdf "Learning representations by back-propagating errors"] <em>Nature</em> <strong>323</strong> (6088): 533–536</ref> It is a ''supervised'' learning technique, meaning that the desired outputs are known beforehand, and the task of the network is to learn to generate the desired outputs from the inputs. | ||
| Line 45: | Line 47: | ||
We first define an error term which is the cross-entropy of the output and target. We use cross-entropy because, in a sense, each output neuron represents a hypothesis about what the input represents, and the activation of the neuron represents a probability that the hypothesis is correct. | We first define an error term which is the cross-entropy of the output and target. We use cross-entropy because, in a sense, each output neuron represents a hypothesis about what the input represents, and the activation of the neuron represents a probability that the hypothesis is correct. | ||
| − | + | [[File:FfBp13.png|center]] | |
The lower the cross entropy, the more accurately the network represents what needs to be learned. | The lower the cross entropy, the more accurately the network represents what needs to be learned. | ||
| Line 51: | Line 53: | ||
Next, we determine how the error changes based on changes to an individual weight from hidden neuron to output neuron: | Next, we determine how the error changes based on changes to an individual weight from hidden neuron to output neuron: | ||
| − | + | [[File:FfBp14.png|center]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | We then want to change | + | We then want to change [[File:FfBp7.png]] slightly in the direction which reduces <em>E</em>, that is, [[File:FfBp15.png]]. This is called ''gradient descent''. |
| − | + | [[File:FfBp16.png|center]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
We do the same thing to find the update rule for the weights between input and hidden neurons: | We do the same thing to find the update rule for the weights between input and hidden neurons: | ||
| − | + | [[File:FfBp17.png|center]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | We then want to change | + | We then want to change [[File:FfBp6.png]] slightly in the direction which reduces <em>E</em>, that is, [[File:FfBp18.png]]: |
| − | + | [[File:FfBp19.png|center]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
== Objections == | == Objections == | ||
| Line 89: | Line 71: | ||
While mathematically sound, the feedforward backpropagation algorithm has been called biologically implausible due to its requirements for neural connections to communicate backwards.<ref><em>Backpropagation: Theory, Architectures, and Applications</em>. Chauvin, Yves; Rumelhart, David E. (1995). Lawrence Erlbaum Associates, Inc. ISBN 0805812598</ref> | While mathematically sound, the feedforward backpropagation algorithm has been called biologically implausible due to its requirements for neural connections to communicate backwards.<ref><em>Backpropagation: Theory, Architectures, and Applications</em>. Chauvin, Yves; Rumelhart, David E. (1995). Lawrence Erlbaum Associates, Inc. ISBN 0805812598</ref> | ||
| − | == References = | + | == References == |
<references/> | <references/> | ||
[[Category: Neural computational models]] | [[Category: Neural computational models]] | ||
| + | |||
| + | </translate> | ||
Latest revision as of 03:14, 24 June 2016
Feedforward backpropagation is an error-driven learning technique popularized in 1986 by David Rumelhart (1942-2011), an American psychologist, Geoffrey Hinton (1947-), a British informatician, and Ronald Williams, an American professor of computer science.[1] It is a supervised learning technique, meaning that the desired outputs are known beforehand, and the task of the network is to learn to generate the desired outputs from the inputs.
Contents
Model
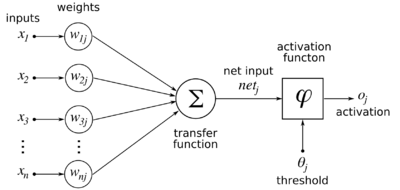
Given a set of k-dimensional inputs with values between 0 and 1 represented as a column vector:
and a nonlinear neuron with (initially random, uniformly distributed between -1 and 1) synaptic weights from the inputs:
then the output of the neuron is defined as follows:
This function has the useful property that
Feedforward backpropagation is typically applied to multiple layers of neurons, where the inputs are called the input layer, the layer of neurons taking the inputs is called the hidden layer, and the next layer of neurons taking their inputs from the outputs of the hidden layer is called the output layer. There is no direct connectivity between the output layer and the input layer.
Derivation
We first define an error term which is the cross-entropy of the output and target. We use cross-entropy because, in a sense, each output neuron represents a hypothesis about what the input represents, and the activation of the neuron represents a probability that the hypothesis is correct.
The lower the cross entropy, the more accurately the network represents what needs to be learned.
Next, we determine how the error changes based on changes to an individual weight from hidden neuron to output neuron:
We do the same thing to find the update rule for the weights between input and hidden neurons:
Objections
While mathematically sound, the feedforward backpropagation algorithm has been called biologically implausible due to its requirements for neural connections to communicate backwards.[2]
References
- ↑ Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J. (October 8, 1986). "Learning representations by back-propagating errors" Nature 323 (6088): 533–536
- ↑ Backpropagation: Theory, Architectures, and Applications. Chauvin, Yves; Rumelhart, David E. (1995). Lawrence Erlbaum Associates, Inc. ISBN 0805812598