Difference between revisions of "Contrastive Hebbian learning"
| Line 21: | Line 21: | ||
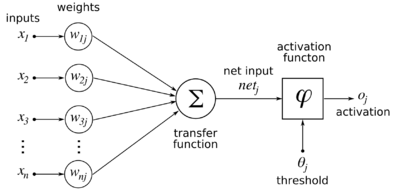
then the output <em>y</em> of the neuron is defined as follows: | then the output <em>y</em> of the neuron is defined as follows: | ||
| − | + | [[File:APRBp1.png|center]] | |
| − | + | ||
| − | + | ||
| − | where | + | where [[File:RBM3.png]] is a sigmoidal function such as that used in ordinary [[feedforward backpropagation]] (we will use the logistic function from that page), and <em>n</em> is the net input of the neuron. During the positive phase, the net is written as [[File:CHL1.png]] with the output being [[File:CHL2.png]], and during the negative phase, the net is written as [[File:CHL3.png]] with the output being [[File:CHL4.png]]. |
| − | Let there be < | + | Let there be <em>N</em> neurons where some of the neurons are simple inputs to the network, some are outputs, with the weight of the connection from neuron <em>i</em> to neuron <em>j</em> being [[File:Sanger2.png]]. Also make sure that [[File:APRBp4.png]], that is, the connections and their weights are symmetric. Obviously if one of the neurons is an input, the connection going into it is useless, but nevertheless this is convenient. |
| − | The positive phase net | + | The positive phase net [[File:CHL5.png]] of neuron <em>j</em> (where <em>j</em> is neither an input neuron nor an output neuron) is computed using a discrete time approximation to the following equation, iteratively applied to all neurons until the nets settle to some equilibrium state. Initially set [[File:CHL5.png]] to 0 for all non-input and non-output neurons. |
| − | + | [[File:CHL6.png|center]] | |
where: | where: | ||
| − | + | [[File:CHL7.png|center]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | where | + | where [[File:CHL8.png|center]] is a target output. Effectively, the output neurons are clamped to their target values, the inputs are applied, and the rest of the neurons are allowed to settle to equilibrium. Note that when equilibrium is reached, [[File:CHL9.png]], and the nets are precisely equal to the weighted sum of their inputs, as expected. |
| − | Next, the negative phase nets | + | Next, the negative phase nets [[File:CHL10.png]] are computed in nearly the same way, except this time start with the nets from the positive phase,<ref>Movellan, Javier R. (April 1991). [http://mplab.ucsd.edu/wp-content/uploads/CHL90.pdf "Contrastive Hebbian learning in the continuous Hopfield model"]. In <em>Connectionist Models: Proceedings of the 1990 Summer School</em>. Morgan Kaufmann Publishers. ISBN 978-1558601567</ref> and the output neurons are not clamped: |
| − | + | [[File:CHL11.png|center]] | |
where | where | ||
| − | + | [[File:CHL12.png|center]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Note that if the weights between pairs of neurons are symmetric, that is, | + | Note that if the weights between pairs of neurons are symmetric, that is, [[File:APRBp4.png]], then the network is guaranteed to settle to an equilibrium state.<ref>Hopfield, J. J. (May 1984). [http://www.pnas.org/content/81/10/3088.full.pdf "Neurons with graded response have collective computational properties like those of two-state neurons"]. <em>Proceedings of the National Academy of Sciences of the United States of America</em>. <strong>81</strong>: 3088-3092</ref> If symmetry is not held, the network will often settle.<ref name=Galland1991>Galland, C. G.; Hinton, G. E. (April 1991). "Deterministic Boltzmann learning in networks with asymmetric connectivity" In <em>Connectionist Models: Proceedings of the 1990 Summer School</em> Morgan Kaufmann Publishers. pp. 39-9 ISBN 978-1558601567</ref> Of course, if <em>i</em> is an input, then [[File:APRBp5.png]] does not exist. |
Once the positive and negative nets of the neurons are determined, the weights are updated according to the following equation: | Once the positive and negative nets of the neurons are determined, the weights are updated according to the following equation: | ||
| − | + | [[File:CHL13.png|center]] | |
| − | where | + | where η is some small learning rate. When the network learns the target, the negative phase exactly cancels out the positive phase, and there is no net change in weight. Also note that [[File:CHL14.png]], meaning that complementary weights go up and down in lockstep. |
== Relation to cross-entropy == | == Relation to cross-entropy == | ||
| − | If, as discussed in the [[feedforward backpropagation]] derivation, the update to the weight is a gradient descent on the cross-entropy of the network, that is, | + | If, as discussed in the [[feedforward backpropagation]] derivation, the update to the weight is a gradient descent on the cross-entropy of the network, that is, [[File:CHL15.png]], then the change in weight due to the positive phase, where the outputs are clamped to the target, results in a lowering of cross-entropy where the output is the target. The change in weight due to the negative phase, however, where the outputs are not the target, results in a raising of cross entropy where the output is not the target. |
This has the effect of "sculpting" the cross-entropy of the network so that it ends up lower where the output is closer to the target, and higher where the output is farther away from the target.<ref>Seung, Sebastian. [http://hebb.mit.edu/courses/9.641/2006/lectures/chl.ppt.pdf "Contrastive Hebbian learning"]. Retrieved Apr 15, 2012.</ref> | This has the effect of "sculpting" the cross-entropy of the network so that it ends up lower where the output is closer to the target, and higher where the output is farther away from the target.<ref>Seung, Sebastian. [http://hebb.mit.edu/courses/9.641/2006/lectures/chl.ppt.pdf "Contrastive Hebbian learning"]. Retrieved Apr 15, 2012.</ref> | ||
Revision as of 19:40, 24 June 2014
Contrastive Hebbian learning is an error-driven learning technique. It is a supervised learning technique, meaning that the desired outputs are known beforehand, and the task of the network is to learn to generate the desired outputs from the inputs.
As opposed to a feedforward network, a recurrent network is allowed to have connections from any neuron to any neuron in any direction. However, unlike Almeida-Pineda recurrent backpropagation, there is no backpropagation of errors; weights are updated purely via local information.
There are two phases to the model, a positive phase, also called the Hebbian or learning phase, and a negative phase, also called the anti-Hebbian or unlearning phase.
Model
Given a set of k-dimensional inputs with values between 0 and 1 represented as a column vector:
and a nonlinear neuron with (initially random, uniformly distributed between -1 and 1) synaptic weights from the inputs:
then the output y of the neuron is defined as follows:
where:
where
Once the positive and negative nets of the neurons are determined, the weights are updated according to the following equation:
Relation to cross-entropy
If, as discussed in the feedforward backpropagation derivation, the update to the weight is a gradient descent on the cross-entropy of the network, that is,This has the effect of "sculpting" the cross-entropy of the network so that it ends up lower where the output is closer to the target, and higher where the output is farther away from the target.[4]
Biological plausibility
Unlike in backpropagation modes such as feedforward backpropagation or Almeida-Pineda recurrent backpropagation, Contrastive Hebbian learning does not depend on the sending of error information backwards along connections. All the information needed to alter the weight is available locally. However, there are two phases to the model. There is some speculation that this has an analog in biological processing, where the negative phase comes first, followed by a positive phase some 300 milliseconds later.[5]
Contrastive Hebbian learning requires that weights be symmetric. There is some evidence that there are symmetric connections between cortical areas in the brain.[6] In addition, symmetric connectivity between individual neurons does not appear to be critical; as long as there is some bidirectional connectivity between some neurons, error signals can be obtained indirectly by the network.[3]
References
- ↑ Movellan, Javier R. (April 1991). "Contrastive Hebbian learning in the continuous Hopfield model". In Connectionist Models: Proceedings of the 1990 Summer School. Morgan Kaufmann Publishers. ISBN 978-1558601567
- ↑ Hopfield, J. J. (May 1984). "Neurons with graded response have collective computational properties like those of two-state neurons". Proceedings of the National Academy of Sciences of the United States of America. 81: 3088-3092
- ↑ 3.0 3.1 Galland, C. G.; Hinton, G. E. (April 1991). "Deterministic Boltzmann learning in networks with asymmetric connectivity" In Connectionist Models: Proceedings of the 1990 Summer School Morgan Kaufmann Publishers. pp. 39-9 ISBN 978-1558601567
- ↑ Seung, Sebastian. "Contrastive Hebbian learning". Retrieved Apr 15, 2012.
- ↑ O'Reilly, Randall C. (1996). "Biologically plausible error-driven learning using local activation differences: the general recirculation algorithm" Neural Computation 8 (5): 895-938
- ↑ Felleman, D. J.; Van Essen, D. C. (1991). Distributed hierarchical processing in the primate cerebral cortex Cerebral Cortex (1): 1-47