Almeida-Pineda recurrent backpropagation
Almeida-Pineda recurrent backpropagation is an error-driven learning technique developed in 1987 by Luis B. Almeida[1] and Fernando J. Pineda.[2][3] It is a supervised learning technique, meaning that the desired outputs are known beforehand, and the task of the network is to learn to generate the desired outputs from the inputs.
As opposed to a feedforward network, a recurrent network is allowed to have connections from any neuron to any neuron in any direction.
Model
Given a set of k-dimensional inputs represented as a column vector:
and a nonlinear neuron with (initially random, uniformly distributed between -1 and 1) synaptic weights from the inputs:
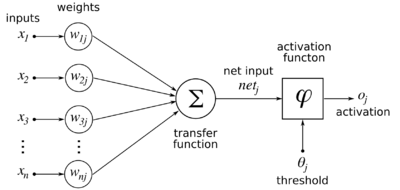
then the output <math>y</math> of the neuron is defined as follows:
y &= \varphi \left ( n \right )
\end{align}</math>where <math>\varphi \left ( \cdot \right )</math> is a sigmoidal function such as that used in ordinary feedforward backpropagation (we will use the logistic function from that page), and <math>n</math> is the net input of the neuron, calculated as follows. Assuming <math>N</math> neurons where <math>k</math> of the neurons are simple inputs to the network, with the weight of the connection from neuron <math>i</math> to neuron <math>j</math> being <math>w_{ij}</math>, the net <math>n_j</math> of neuron <math>j</math> (where <math>j</math> is not an input neuron) is computed using a discrete time approximation to the following equation, iteratively applied to all neurons until the nets settle to some equilibrium state:
\varphi \left ( n_i \right ) & \text{ if } i \text{ is not an input } \\ x_i & \text{ if } i \text{ is an input }
\end{cases}</math>Note that if the weights between pairs of neurons are symmetric, that is, <math>w_{ij} = w_{ji}</math>, then the network provably settles to an equilibrium state.[4] If symmetry is not held, the network will often settle.[5] Of course, if <math>i</math> is an input, then <math>w_{ji}</math> does not exist.
Once the outputs of the neurons are determined, an error phase is run to determine the outputs of the neurons solely for the purpose of weight modification. As above, these outputs are computed using a discrete time approximation to the following equation, iteratively applied to all neurons until the nets settle to some equilibrium state:
where <math>J_j</math> is an error term for neurons which are outputs and have targets <math>t_j</math>:
The weights are then updated according to the following equations:
\frac{\partial E }{\partial w_{ij}} &= - y_j \frac{\mathrm{d} y_j }{\mathrm{d} n_j} \frac{\partial n_j}{\partial w_{ij}} \\ &= - y_j \frac{\mathrm{d} \varphi }{\mathrm{d} n_j} y_i \\ &= - y_j \varphi \left ( n_j \right ) \left ( 1 - \varphi \left ( n_j \right ) \right ) y_i \\ \Delta w_{ij} &= - \eta \frac{\partial E}{\partial w_{ij}} &= - \eta y_j \varphi \left ( n_j \right ) \left ( 1 - \varphi \left ( n_j \right ) \right ) y_i
\end{align}</math>where <math>\eta</math> is some small learning rate.
References
- ↑ Script error: No such module "Citation/CS1". Paywalled.
- ↑ Template:Cite book
- ↑ Script error: No such module "Citation/CS1".
- ↑ Script error: No such module "Citation/CS1".
- ↑ Template:Cite book