Difference between revisions of "Hebb's rule"
| Line 1: | Line 1: | ||
| + | <translate> | ||
| + | |||
'''Hebb's Rule''' or Hebb's postulate attempts to explain "associative learning", in which simultaneous activation of cells leads to pronounced increases in [[Synapse|synaptic]] strength between those cells. Hebb stated: | '''Hebb's Rule''' or Hebb's postulate attempts to explain "associative learning", in which simultaneous activation of cells leads to pronounced increases in [[Synapse|synaptic]] strength between those cells. Hebb stated: | ||
| Line 49: | Line 51: | ||
[[Category: Neural computational models]] | [[Category: Neural computational models]] | ||
| + | |||
| + | </translate> | ||
Latest revision as of 03:15, 24 June 2016
Hebb's Rule or Hebb's postulate attempts to explain "associative learning", in which simultaneous activation of cells leads to pronounced increases in synaptic strength between those cells. Hebb stated:
- Let us assume that the persistence or repetition of a reverberatory activity (or "trace") tends to induce lasting cellular changes that add to its stability.… When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A's efficiency, as one of the cells firing B, is increased.[1]
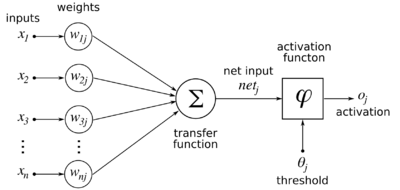
Model
Given a set of k-dimensional inputs represented as a column vector:
and a linear neuron with (initially random, uniformly distributed between -1 and 1) synaptic weights from the inputs:
then the output the neuron is defined as follows:
Hebb's rule gives the update rule which is applied after an input pattern is presented:
where η is some small fixed learning rate.
It should be clear that given the same input applied over and over, the weights will continue to grow without bound. One solution is to limit the size of the weights. Another solution is to normalize the weights after every presentation:
Normalizing the weights leads to Oja's rule.
Hebb's rule and correlation
Instead of updating the weights after each input pattern, we can also update the weights after all input patterns. Suppose that there are N input patterns. If we set the learning rate η equal to 1/N, then the update rule becomes
References
- ↑ Hebb, D. O. (1949). The Organization of Behavior: A Neuropsychological Theory ISBN 978-0805843002.